Definición de Grafo:

•          Un grafo G es una tupla G= (V, A), donde V es un conjunto no vacío de vértices o nodos y A es un conjunto de aristas o arcos.

•          Cada arista es un par (v, w), donde v, w ∈ V.

Tipos de grafos

•          Grafo no dirigido.
Las aristas no están ordenadas:
   (v, w) = (w, v)

     

 

•          Grafos dirigidos (o digrafos).
Las aristas son pares ordenados:
                <v, w> ≠ <w, v>

                <v, w> ⇒ w = cabeza de la arista, v = cola.

           

          

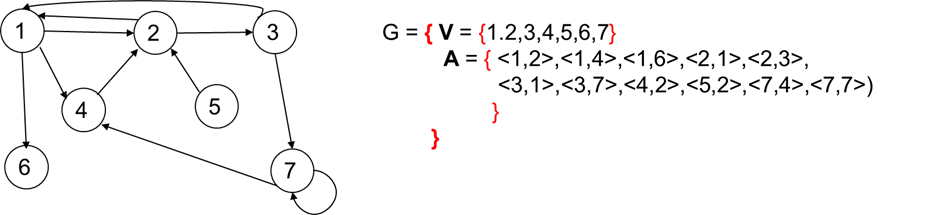
Terminología de grafos.

•          Nodos adyacentes a un nodo v: todos los nodos unidos a v mediante una arista.

•          En grafos dirigidos:

–         Nodos adyacentes a v: todos los w con <v, w> ∈ A.

–         Nodos adyacentes de v: todos los u con <u, v> ∈ A.

–         Un grafo está etiquetado si cada arista tiene asociada una etiqueta o valor de cierto tipo.

•          Grafo con pesos o ponderado: es un grafo etiquetado con valores numéricos.

•          Grafo etiquetado: G= (V, A, W), con W: A → TipoEtiq

 Grafos dirigidos etiquetados con pesos.

 

•          Camino de un vértice w₁ a w_q: es una secuencia w₁, w₂, ..., w_q ∈ V, tal que todas las aristas (w₁, w₂), (w₂, w₃), ..., (w_q-1, w_q) ∈ A.

•          Longitud de un camino: número de aristas del camino = nº de nodos -1.

•          Camino simple: aquel en el que todos los vértices son distintos (excepto el primero y el último que pueden ser iguales).

•          Ciclo: es un camino en el cual el primer y el último vértice son iguales. En grafos no dirigidos las aristas deben ser diferentes.

•          Se llama ciclo simple si el camino es simple.

   

Definición de Subgrafo:

Un subgrafo de G=(V, A) es un grafo G’=(V’, A’) tal que V’ ⊆ V y A’ ⊆ A.

Dados dos vértices v, w, se dice que están conectados si existe un camino de v a w.

Un grafo es conexo (o conectado) si hay un camino entre cualquier par de vértices.

Si es un grafo dirigido, se llama fuertemente conexo.

Un componente (fuertemente) conexo de un grafo G es un subgrafo maximal (fuertemente) conexo.

•          Un grafo es completo si existe una arista entre cualquier par de vértices.

•          Para n nodos, ¿cuántas aristas tendrá un grafo completo (dirigido o no dirigido)?

•          Grado de un vértice v: número de arcos que inciden en él.

•          Para grafos dirigidos:

        - Grado de entrada de v: nº de aristas con <x, v>

         - Grado de salida de v: nº de aristas con <v, x>

Operaciones elementales con grafos:

•          Crear un grafo vacío (o con n vértices).

•          Insertar un nodo o una arista.

•          Eliminar un nodo o arista.

•          Consultar si existe una arista (obtener la etiqueta).

Iteradores sobre las aristas de un nodo:

 para todo nodo w adyacente a v hacer
                 acción sobre w

 para todo nodo w adyacente de v hacer
                 acción sobre w      (Mucho menos frecuente)