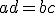Con todo lo anterior aceptamos la existencia del conjunto de los números reales, 
, junto con las siguientes propiedades:
- En se tienen dos operaciones binarias, a saber, suma “+” y producto “
”. - Para cualesquiera números reales x e y , se satisfacen las siguientes propiedades:
x+y es un número real.
xy es un número real.
A estas propiedades se le conoce como la propiedades de cerradura para la suma y el producto.
En los números reales existe una relación de igualdad “=” que cumple las siguientes propiedades. Para cualesquiera números reales , se tiene:
| a=a | Propiedad reflexiva |
| Si a=b, entonces b=a | Propiedad simétrica |
| Si a=b y b=c, entonces a=c | Propiedad transitiva |
|
Si a=b, entonces
|
Propiedades de consistencia de la suma y el producto. |
Se sabe que 2+6=6+2, 3(5+2) = 3(5)+(2), 
y que (3+5)+8=3+(5+8), y así sucesivamente. Estas propiedades de los números reales están sustentadas en lo que se le conoce como Axiomas de Campo. Estos axiomas (proposiciones que NO requieren demostración) nos ayudan a entender el proceso deductivo de las matemáticas de los números.
Si a, b, c son números reales cualesquiera, se tienen los siguientes axiomas de los números reales:
| Axiomas de los números reales | |
|
a+b=b+a ab=ba |
Propiedad Conmutativa |
|
(a+b)+c=a+(b+c) (ab)c=a(bc) |
Propiedad asociativa |
|
a(b+c)=ab+ac (b+c)a=ba+ca |
Propiedad distributiva |
| Existe un único 0 tal que: a+0=0+a=a | Existencia del neutro aditivo |
|
Existe un único 1 tal que:
|
Existencia del neutro multiplicativo |
|
Para cada a existe un único número real -a tal que: a+(-a)=0 |
Inverso aditivo |
|
Si
NOTA: Se puede escribir |
Inverso multiplicativo |
, entonces existe un único número real 
tal que:
en lugar de 
La sustracción es la operación inversa de la adición; para restar un número de otro simplemente sumamos el inverso aditivo de ese número. Esto es,
a-b=a+(-b)
Algunas propiedades que podemos mencionar de los números con signo negativo son:
- (-1)a=-a
- -(-a)=a
- (-a)b=a(-b)=-(ab)
- (-a)(-b)=ab
- -(a+b)=-a-b
- -(a-b)=b-a
En la propiedad del inverso aditivo, NO debemos de suponer que -a es un número negativo. Esto ya que depende del valor de a. Por ejemplo: si a=5, entonces , -a=-5, pero si a=-5, entonces -a=-(-5)=5 que resulta ser un número positivo.
La operación división es la operación inversa de la multiplicación; para dividir un número multiplicamos por el inverso de ese número. Así, si 
, entonces, por definición,
Escribimos 
simplemente como 
. Al valor de a se le conoce como el numerador y el valor de b se le conoce como el denominador. A continuación, se presentan algunas propiedades que cumplen las fracciones.
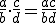
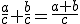
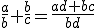
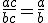
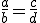si y sólo si 