Un exponente entero positivo indica cuantas veces el factor, llamado base, se multiplicará por sí mismo. El concepto es muy útil para expresar grandes cantidades de manera corta. El resultado obtenido de elevar la base a un exponente se le llama potencia. De manera simbólica para representar a una potencia es la siguiente:
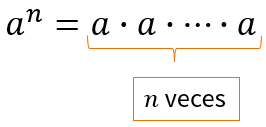

Ejemplos: Con la notación anterior tenemos:
Para realizar operaciones con potencias deberán seguirse ciertas leyes. Para ello, sean a y b números reales m y n números enteros, entonces se cumplen las siguientes igualdades:

A continuación se presentan otras dos leyes que serán de utilidad para simplificar expresiones con exponentes negativos.
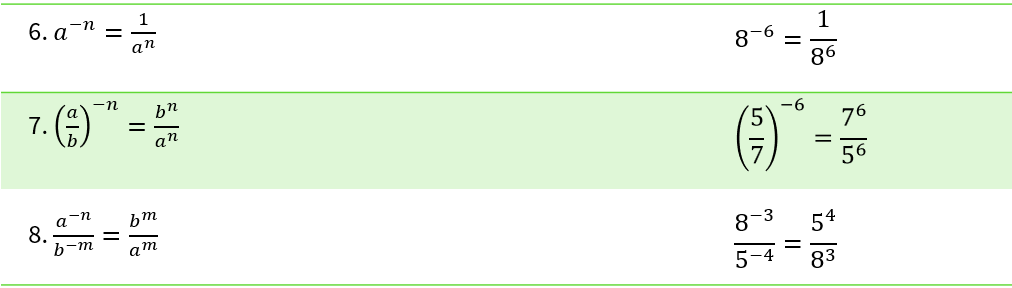
Para el caso en el que exponente sea 0 se tiene lo siguiente:
Si a≠0 es un número real, entonces
![]()
a^0=1
Ejemplos:
I. Evaluar cada una de las siguientes expresiones:
II. Aplica las leyes de los exponentes y expresa los resultados sin exponentes negativos.


