Hemos visto el significado de 
con n un número entero. Para dar el significado de 
, cuyo exponente es un número racional, necesitaremos analizar a los radicales.
Definición: Si n es un entero positivo, entonces la raíz n-ésima principal de a se define como:
si y sólo si 
.
Si n es par, se debe de considerar que a≥0 y b≥0.
Observaciones:
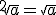
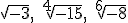no están definidos.
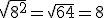, pero 
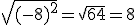. Así, 
se cumple siempre y cuando 
.
Algunas propiedades que cumplen las raíces n-ésimas se enlistan en la siguiente tabla.
Con todo lo anterior tenemos la siguiente definición.
Definición: Para cualquier exponente racional m/n, donde m y n son enteros y n>0, definimos:
.
Si n es par es necesario considerar que a≥0.
Con esta definición, todas las leyes de los exponentes son válidas para los exponentes racionales.
Ejemplo: Utiliza las leyes de los exponentes y radicales para simplificar las siguientes expresiones.
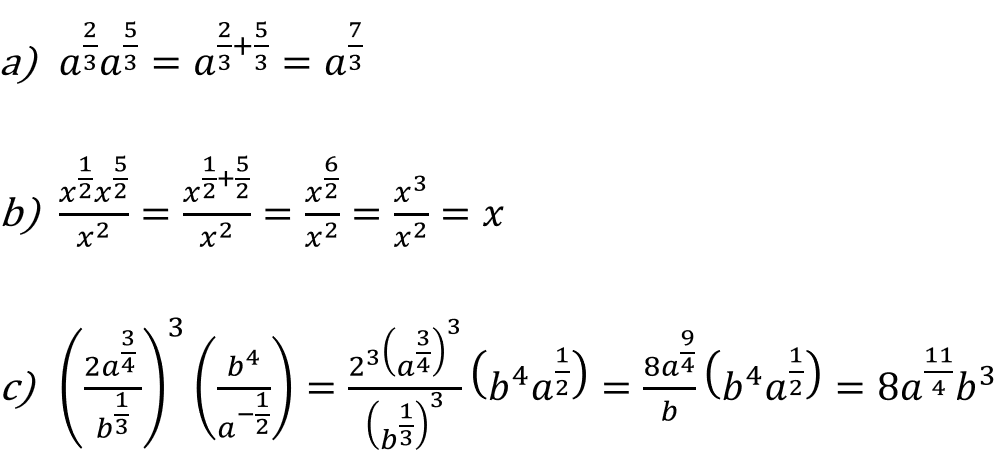
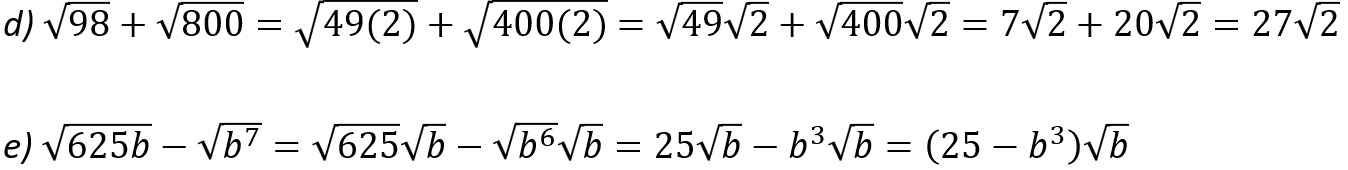
Los siguientes vídeos muestran el uso de las propiedades de los radicales.