Fuerzas paralelas en el mismo sentido

observando el siguiente diagrama:

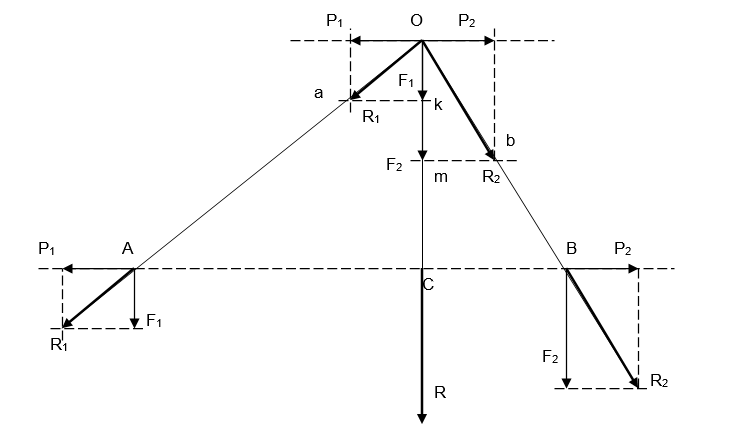
No se puede utilizar directamente la regla del paralelogramo de fuerzas para componer dos fuerzas paralelas F1 y F2 aplicadas en los puntos A y B de un sólido. Entonces se aplica el procedimiento siguiente:

1. Aplicamos en los puntos A y B dos fuerzas P1 y P2 de igual magnitud y de sentido contrario. P1 = - P2
2. Componiendo las fuerzas F1 y P1, F2 y P2 obtenemos dos fuerzas R1 y R2 cuyas líneas de acción se intersectan en el punto O.
3. Trasladamos las fuerzas R1 y R2 al punto O y las descomponemos para obtener las fuerzas F’1 y P’1, F’2 y P’2.
4. Como P’1 y P’2 pueden anularse, obtenemos las fuerzas F’1 y F’2 dirigidas a lo largo de una recta cuya línea de acción se intersecta con el segmento AB en el punto C.
5. Trasladamos F’1 y F’2 al punto C.
6. Podemos hacer F’1 + F’2 = R.

Posición del punto C

 

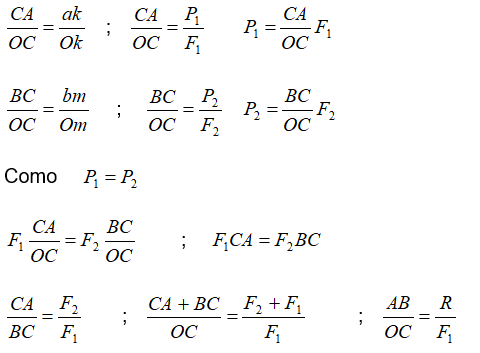
Por lo tanto podemos concluir:

La resultante de dos fuerzas paralelas, de sentidos iguales aplicadas a un cuerpo sólido es de la misma dirección y sentido que las fuerzas componentes, paralela a éstas y su módulo es igual a la suma de los módulos de las fuerzas componentes. La línea de acción de la resultante R pasa entre los puntos de aplicación de las componentes a una distancia de éstas, inversamente proporcional a las fuerzas.

Fuerzas paralelas en sentido contrario

A partir del diagrama presentado a continuación podemos observar lo siguiente:

  

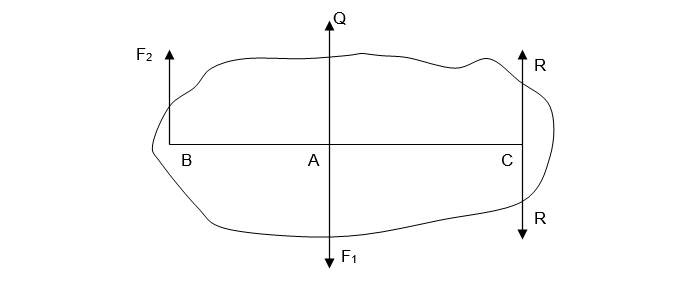
Suponiendo que en los puntos A  y  B   de un cuerpo sólido están aplicadas dos fuerzas paralelas F1 y F2 dirigidas en sentidos opuestos; y que además, los módulos de las fuerzas F1 y F2 son tal que F1 > F2.

Por lo anterior podemos decir que, la resultante de dos fuerzas paralelas, de sentidos contrarios aplicadas a un cuerpo sólido es de la misma dirección que la mayor de las componentes, es paralela a éstas y su módulo es la diferencia de los módulos de las componentes. La línea de acción de la resultante pasa fuera del segmento que une los puntos de aplicación de las fuerzas componentes, la distancia hasta estos puntos es inversamente proporcional a las fuerzas.

Si las fuerzas paralelas son varias, la resultante puede hallarse mediante la aplicación consecutiva de la regla anterior.