Teorema 1

Un par de fuerzas aplicado a un cuerpo rígido puede ser sustituido, sin variar su acción sobre este cuerpo, por otro par coplanar cualquiera del mismo momento.

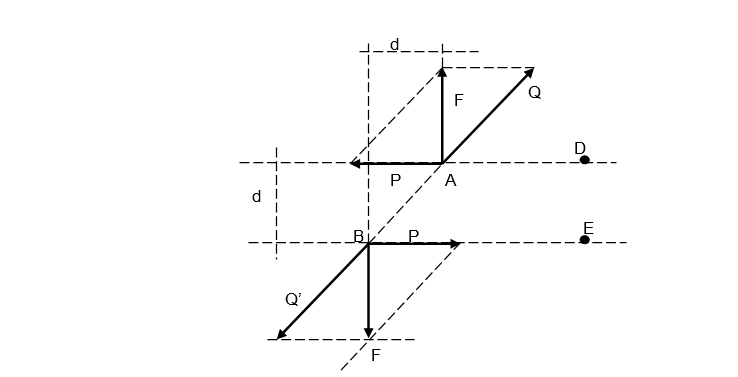
Sea el par F, F’ con un brazo d1.

• Se trazan dos paralelas AD y BE separadas d2 hasta cortar a F y F’.
• Se descomponen F y F’ en P, Q  y  P’ y Q’.
• P=-P’  y  como Q= -Q’ y además son colineales Q  y Q’ se anulan.
• Solamente quedan P y P’ separadas d2.

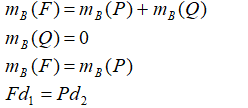
De lo anterior se deducen las propiedades siguientes:

1. Un par dado puede trasladarse a cualquier lugar del plano de acción de éste sin variar su acción sobre el cuerpo.
2. En un par dado se puede cambiar arbitrariamente los módulos de las fuerzas o la longitud del brazo sin variar la acción que este par ejerce sobre el cuerpo y manteniendo constante su momento. Por lo tanto. Dos pares coplanares de momentos iguales son equivalentes pues se puede transformar uno en el otro.

Por lo anterior, frecuentemente un par se representa por el símbolo  aplicado en el punto de aplicación del par.

Teorema 2

La acción de un par de fuerzas sobre un cuerpo sólido no varía si el par se traslada del plano en cuestión a otro plano cualquiera paralelo al original.

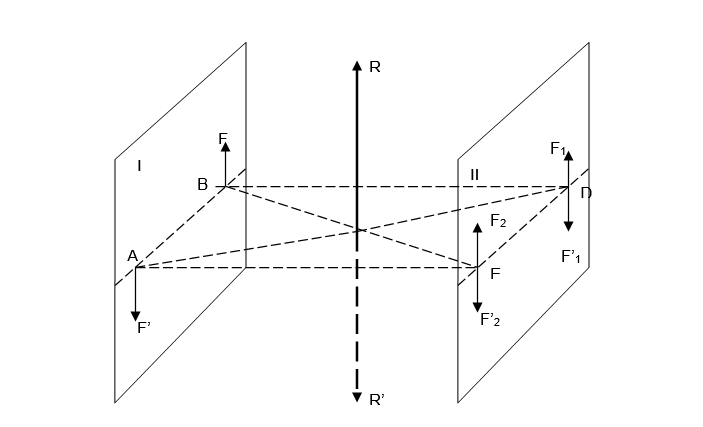
Las líneas AB  y ED son iguales. Ahora en ED hay cuatro fuerzas.

Entonces se tiene:

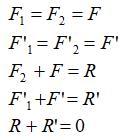
Hasta aquí quedan F1 y F'2 que forman un par igual al anterior, pero en el plano II.

Podemos decir que, dos planos de momentos iguales que se encuentran en planos paralelos son también equivalentes.